Solving equations involves finding the value of an unknown variable; worksheets often present problems where variables appear on both sides, demanding careful manipulation.
What are Equations with Variables on Both Sides?
Equations with variables on both sides are algebraic statements where the unknown value (represented by a variable, like ‘x’) isn’t isolated initially. Instead, terms containing the variable appear on both the left and right sides of the equals sign. For example, an equation like 5x ‒ 2 = 2x + 7 demonstrates this concept. These equations require a strategic approach to isolate the variable and determine its value;
Worksheets focusing on these equations often present a series of problems, starting with simpler linear equations and progressing to more complex scenarios involving distribution or fractions. The core skill is manipulating the equation using inverse operations – addition, subtraction, multiplication, and division – to systematically move variable terms to one side and constant terms to the other, ultimately revealing the solution.
Why are these Equations Important?
Mastering equations with variables on both sides is fundamental to algebraic proficiency and serves as a crucial stepping stone for more advanced mathematical concepts. These equations aren’t merely abstract exercises; they model real-world scenarios where relationships between quantities need to be determined. Understanding how to solve them builds problem-solving skills applicable across various disciplines.
Worksheet practice reinforces the logical thinking required to manipulate equations correctly. The ability to combine like terms, apply inverse operations, and check solutions are vital skills. Furthermore, proficiency in solving these equations prepares students for tackling more complex algebraic challenges, including systems of equations and inequalities, ultimately strengthening their mathematical foundation.

Understanding the Core Concept
The central idea revolves around maintaining equation balance; any operation performed on one side must be mirrored on the other to isolate the variable.
The Goal: Isolating the Variable
The primary objective when tackling equations with variables on both sides is to strategically manipulate the equation until the variable stands alone on one side. This means employing inverse operations – addition/subtraction, multiplication/division – to systematically “undo” the operations affecting the variable.
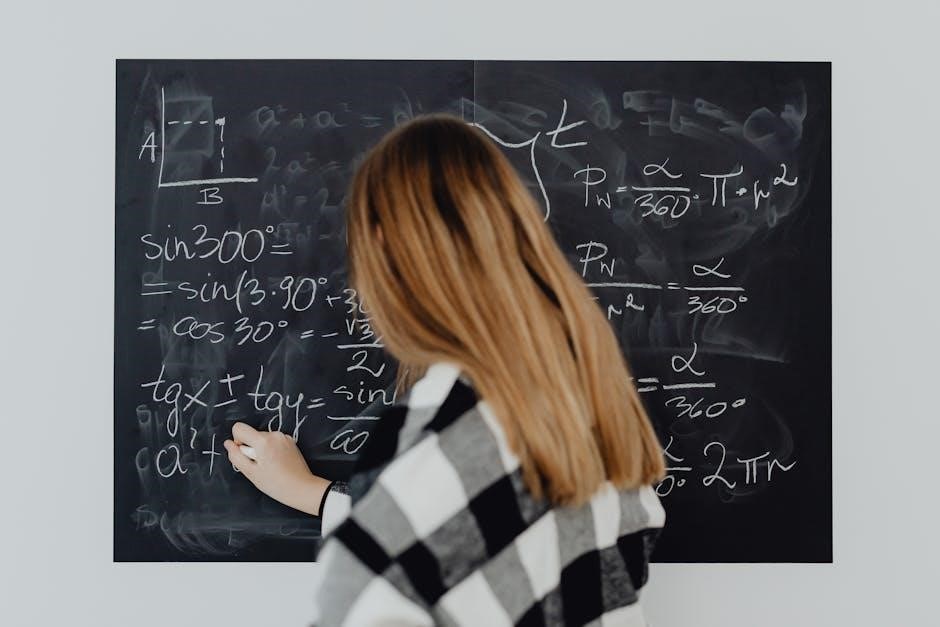
Worksheets emphasize this process, presenting equations where terms with the variable exist on both sides. The goal isn’t simply to find *a* number that makes the equation true, but to pinpoint the *specific* value that satisfies the equation. Think of it like a puzzle; you’re carefully dismantling the equation piece by piece, using mathematical rules, until only the variable remains, revealing its solution. Successfully isolating the variable demonstrates a complete understanding of equation-solving principles.
Using Inverse Operations
Inverse operations are the cornerstone of solving equations. They “undo” each other – addition cancels subtraction, multiplication reverses division, and so on. When worksheets present equations with variables on both sides, applying inverse operations is crucial for moving terms around and simplifying the equation.
For example, if a term is being added to the variable, you subtract it from both sides. This maintains the equation’s balance. Worksheets often require multiple steps, combining like terms after using inverse operations. Remember, whatever operation is performed on one side must be mirrored on the other to preserve equality. Mastering inverse operations is fundamental to successfully navigating these types of equations and finding the correct solution.

Step-by-Step Solving Process
Worksheets guide students through a structured approach: simplify, move variables, isolate the variable, and crucially, check the solution for accuracy.
Step 1: Simplifying Each Side
Before tackling variables on both sides, worksheets emphasize simplifying each side of the equation independently. This involves combining like terms – those with the same variable and those that are constants (numbers). For example, if an equation presents ‘3x + 5 + 2x’ on one side, it should be simplified to ‘5x + 5’.
Distribution is also a key simplification step, as seen in examples provided. If you encounter terms like ‘2(x + 3)’, you must multiply the 2 by both the ‘x’ and the ‘3’, resulting in ‘2x + 6’.
Worksheets often begin with these simpler simplification exercises to build a solid foundation before introducing the more complex step of moving variables across the equals sign. Mastering this initial step is crucial for success.
Step 2: Moving Variables to One Side
Once each side is simplified, worksheets guide students to consolidate variable terms. This is achieved using inverse operations – performing the opposite mathematical action. If ‘2x’ is on the left and ‘5x’ is on the right, subtract ‘2x’ from both sides. This leaves ‘0’ on the left and ‘3x’ on the right.
The goal is to isolate the variable term on a single side of the equation. Worksheets consistently reinforce the principle of maintaining balance; whatever operation is applied to one side must be applied to the other.
This step often involves careful attention to signs (positive and negative) to avoid errors. Practice with worksheets builds proficiency in strategically moving variables.

Step 3: Isolating the Variable
After consolidating variables, worksheets emphasize isolating the variable itself. If the equation now reads ‘3x = 9’, the variable ‘x’ is multiplied by 3. To isolate ‘x’, perform the inverse operation: division. Divide both sides of the equation by 3.
This results in ‘x = 3’, revealing the solution. Worksheets frequently present equations requiring multiple steps, building upon previous skills. Students learn to systematically undo operations, working backwards from the order of operations (PEMDAS).
Consistent practice with worksheet problems reinforces the concept of maintaining equation balance throughout the isolation process, leading to accurate solutions.
Step 4: Checking Your Solution
Worksheets consistently highlight the crucial final step: checking your solution. Once a value for the variable is found, substitute it back into the original equation. This verifies the solution’s accuracy. For example, if solving for ‘x’ yielded ‘x = 3’ in the equation ‘5x ⏤ 2 = 2x + 4’, substitute 3 for ‘x’.
This yields ‘5(3) ‒ 2 = 2(3) + 4’, simplifying to ‘13 = 10’, which is incorrect. This indicates an error in the solving process, prompting a review of each step.
Worksheets emphasize this verification as a vital habit, building confidence and minimizing careless mistakes.
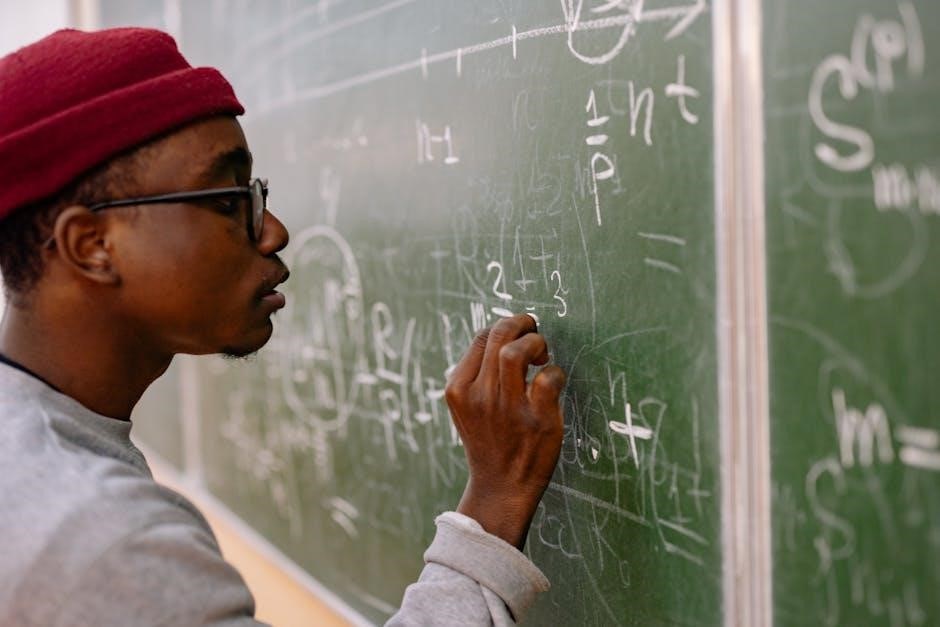
Types of Equations & Examples
Worksheets present linear equations, those with distribution, and even equations involving fractions, all requiring variables to be isolated on both sides.
Linear Equations with Variables on Both Sides
Linear equations featuring variables on both sides are a cornerstone of algebraic problem-solving, frequently appearing on worksheets designed for practice. These equations, as exemplified in resources like Corbettmaths’ Video 113, require students to skillfully manipulate terms to isolate the variable. The core strategy involves combining like terms – moving all variable terms to one side of the equation and constant terms to the other.
Worksheets often begin with simpler examples, progressing to those with negative coefficients or larger numerical values to adjust difficulty. The goal remains consistent: to achieve a balanced equation where the variable stands alone, revealing its solution. Problems typically resolve to integer answers, reinforcing foundational skills. Mastering these equations builds a strong base for tackling more complex algebraic concepts.
Equations with Distribution
Equations requiring distribution add a layer of complexity to solving for variables, commonly found within practice worksheets. Before isolating the variable, students must first apply the distributive property to eliminate parentheses. This involves multiplying the term outside the parentheses by each term inside, effectively expanding the expression.
Following distribution, the equation then resembles a standard linear equation with variables on both sides, demanding the familiar steps of combining like terms and using inverse operations. Worksheets often present equations where distribution is necessary on one or both sides, increasing the challenge. Adjusting the difficulty can involve larger coefficients or more complex distributions. Successfully navigating these equations demonstrates a deeper understanding of algebraic manipulation.
Equations with Fractions
Equations involving fractions present a unique challenge when solving for variables, frequently appearing in advanced worksheet exercises. A common strategy is to eliminate the fractions by multiplying both sides of the equation by the least common multiple (LCM) of the denominators. This transforms the equation into one without fractions, simplifying the process.
Once the fractions are removed, the equation typically resembles a linear equation with variables on both sides, requiring the application of familiar techniques like combining like terms and utilizing inverse operations. Worksheets often include equations with fractions on one or both sides, demanding proficiency in fraction manipulation. Increasing difficulty involves larger denominators or fractions combined with distribution.

Resources: Worksheets & Practice
Numerous worksheets are available online, including Corbettmaths’ resources (Video 113), offering practice solving equations with variables on both sides, adjustable for difficulty.
Corbettmaths Equations: Letters on Both Sides (Video 113)
Corbettmaths provides an excellent Video 113 specifically dedicated to tackling equations where variables appear on both sides of the equal sign. This resource is invaluable for visual learners, walking through the process step-by-step with clear explanations and examples. Accompanying the video are practice questions, categorized into three levels of difficulty – ensuring students can build confidence progressively.
Question sets include solving various linear equations, those requiring distribution, and even equations involving fractions. The problems are designed to result in integer solutions, simplifying the initial learning curve. Teachers and students can tailor the challenge by adjusting the numerical values, introducing negative coefficients, or altering the equation’s structure. This adaptability makes it a versatile tool for diverse learning needs and skill levels. The focus is on combining like terms and applying inverse operations, mirroring the logic of two-step equations.
Solving Equations Worksheet PDF Availability
Numerous online resources offer solving equations worksheets in PDF format, catering to various skill levels and learning preferences. These worksheets typically present a series of equations with variables on both sides, requiring students to apply algebraic manipulation to isolate the variable and determine its value. Many platforms provide answer keys for self-assessment and immediate feedback.
Worksheets often include a progression of difficulty, starting with simpler linear equations and advancing to those involving distribution or fractions. The availability of PDF format allows for easy printing and offline practice, making them ideal for classroom assignments or independent study. Some resources offer customizable worksheets, enabling teachers to tailor the content to specific student needs. These resources are designed to reinforce the concepts taught in videos like Corbettmaths’ Video 113, providing ample opportunity for practice and mastery.
Adjusting Difficulty Levels in Worksheets
Worksheet difficulty can be readily adjusted to suit individual student needs when practicing solving equations with variables on both sides. Increasing the size of the numerical values within the equations presents a greater computational challenge, demanding more precise arithmetic skills. Introducing negative coefficients adds another layer of complexity, requiring careful attention to sign rules during manipulation.
Furthermore, flipping the sides of the equation – presenting the variable terms on the right and constants on the left – can test a student’s understanding of the underlying principles. Worksheets focusing on distribution or incorporating fractional coefficients represent further increases in difficulty. By strategically modifying these elements, educators can create targeted practice opportunities, ensuring students are appropriately challenged and supported in their learning journey, building upon concepts from resources like Corbettmaths.

Common Mistakes to Avoid
Students often forget to apply operations to both sides, or incorrectly combine like terms when solving equations; careful practice with worksheets helps prevent these errors.
Forgetting to Perform the Same Operation on Both Sides
A prevalent error when tackling equations with variables on both sides is neglecting to execute the same mathematical operation on both sides of the equation. Maintaining balance is paramount; think of an equation as a perfectly balanced scale. If you add or subtract a value from one side, you must do the same to the other to preserve the equality.
Worksheets frequently highlight this mistake. For instance, if you’re adding 21 to isolate a term, remember to add 21 to both sides. Failing to do so disrupts the equation’s balance, leading to an incorrect solution. This seemingly small oversight can drastically alter the outcome. Consistent practice with solving equations, utilizing provided worksheets, reinforces this crucial principle and minimizes this common error.
Incorrectly Combining Like Terms
A frequent stumbling block when solving equations, particularly those with variables on both sides, is the improper combination of like terms. Students sometimes attempt to combine terms that aren’t comparable – for example, adding a variable term to a constant number. Worksheets emphasize the importance of identifying and grouping similar terms before applying inverse operations.
Remember, only terms with the same variable and exponent can be combined. For example, 5x and 2x are like terms, but 5x and 7 are not. Incorrectly combining these leads to a flawed equation and an inaccurate solution. Careful attention to detail and consistent practice, using resources like solving equations worksheets, are vital to mastering this fundamental algebraic skill.
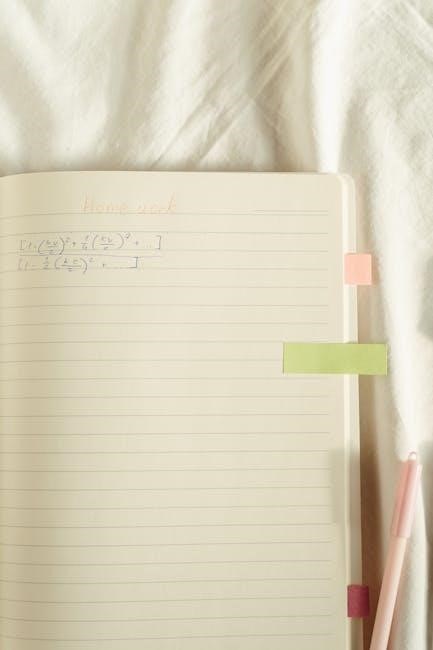
Advanced Techniques
Mastering equation solving extends to negative coefficients and larger values; worksheets provide practice in manipulating these, building confidence and problem-solving skills.
Solving Equations with Negative Coefficients
Equations featuring negative coefficients introduce an added layer of complexity, requiring careful attention to sign rules during each manipulation step. Worksheets dedicated to this skill often begin with simpler examples, gradually increasing the difficulty as students gain proficiency. Remember that distributing a negative sign changes the sign of every term within the parentheses.
When moving terms across the equals sign, be especially mindful of maintaining the correct sign. For instance, adding a negative number is equivalent to subtracting a positive number. Practice with worksheets helps solidify these concepts. Adjusting difficulty involves increasing the magnitude of the coefficients or incorporating more terms, ensuring a robust understanding of algebraic principles. These problems resolve to integers, offering a clear path to verification.
Dealing with Larger Values
As values within equations increase, the potential for arithmetic errors also rises, demanding heightened precision and careful calculation. Worksheets designed to challenge students often incorporate larger numbers to simulate real-world scenarios and build computational fluency. Maintaining organization is crucial; clearly showing each step minimizes mistakes and facilitates error checking.
These larger values don’t alter the fundamental solving process – combining like terms and utilizing inverse operations remain key. However, the increased complexity necessitates a stronger grasp of these concepts. Difficulty can be adjusted by increasing the size of the values, introducing negative coefficients, or flipping the sides of the equation. Remember, all problems should resolve to integers for straightforward verification.

Applications in Real-World Scenarios
Equations model numerous real-world problems, from calculating distances to determining costs; worksheets prepare students to apply these skills to practical situations effectively.
Using Equations to Model Problems
Translating word problems into algebraic equations is a crucial skill. Many real-world scenarios can be represented using equations with variables on both sides, requiring students to identify the unknowns and relationships between them. For instance, consider two competing cell phone plans with different monthly fees and per-minute charges.
Setting up an equation to determine when the costs are equal allows for a practical application of solving equations. Worksheets focusing on these types of problems help students develop their ability to abstract information from a context and represent it mathematically. This process reinforces understanding and builds confidence in tackling more complex scenarios.
Successfully modeling problems demonstrates a deeper comprehension of the underlying mathematical concepts, moving beyond rote memorization to genuine problem-solving ability.
Problem-Solving Strategies
Effective problem-solving with equations requires a systematic approach. Begin by carefully reading the problem and identifying the unknown variable. Next, translate the given information into an algebraic equation, ensuring variables appear on both sides if the scenario dictates. Simplifying each side individually—combining like terms—is a vital first step.
Then, strategically move variable terms to one side of the equation using inverse operations, maintaining balance by applying the same operation to both sides. Isolate the variable to find its value, and crucially, check your solution by substituting it back into the original equation.
Worksheets provide ample practice, reinforcing these strategies and building fluency. Remember, consistent application of these steps leads to accuracy and confidence.